There's a method in pygame to draw an arbitrary polygon. It takes in a list of points and a color and creates a filled-in polygon with corners at those locations. But this isn't very convenient for drawing a simple regular polygon like a simple honeycomb hexagon, or even a 4-sided diamond.
In order to do this generically for all polygons, you'll have to think back to your trigonometry. But first I'll give the code to do this and then pick it apart with the explanation afterwards:
def drawRegularPolygon(surface, color, numSides, tiltAngle, x, y, radius):
pts = []
for i in range(numSides):
x = x + radius * math.cos(tiltAngle + math.pi * 2 * i / numSides)
y = y + radius * math.sin(tiltAngle + math.pi * 2 * i / numSides)
pts.append([int(x), int(y)])
pygame.draw.polygon(surf, color, pts)
# It's a red stop sign
drawRegularPolygon(screen, (255, 0, 0), 8, math.pi / 16, 100, 100, 50)
The key here is the sine and cosine trigonometric functions, which, if you remember back to high school trigonometry, give the ratio of lol don't panic, no one remembers.
But here's a quick picture of everything you need to know, in terms of using them in graphics:
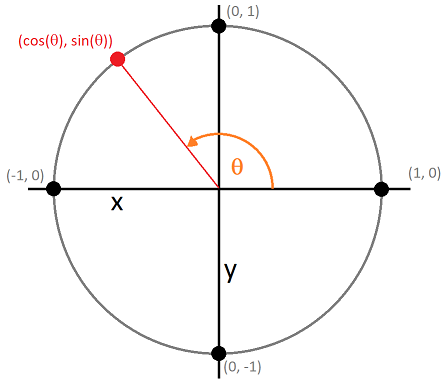
Imagine a circle whose radius is exactly length 1. This circle is centered at the origin (0, 0). Now trace along the outer edge of the circle counterclockwise, starting from the 3 o'clock position. The angle of your pencil with respect to where you started is measured in radians. This angle goes from 0 (where you start at 3 o'clock) to 6.28318 (or 2*pi) (where you finish, back in the same position at 3 o'clock).
So for example, when you reach the 9 o'clock position, that radian measure is pi, because it's halfway to 2 pi. When you reach the 6 o'clock position (remember you're moving counter-clockwise), that is 1.5 * pi (or 75% of 2 * pi).
In this scenario, cosine and sine are functions that convert that angle measurement into x and y coordinates.
| [cos(0), sin(0)] | [1, 0] | 3 o'clock |
| [cos(pi / 2), sin(pi / 2)] | [0, 1] | 12 o'clock |
| [cos(pi), sin(pi)] | [-1, 0] | 9 o'clock |
| [cos(1.5 * pi), sin(1.5 * pi)] | [0, -1] | 6 o'clock |
| [cos(2 * pi), sin(2 * pi)] | [1, 0] | 3 o'clock again |
| [cos(2 * pi / 12), sin(2 * pi / 12)] | [0.866, 0.5] | 2 o'clock |
To get the coordinates of a regular polygon with n sides, you need to draw n points that are evenly spaced out on a circle. We can do this by loop from 0 to n and divide by n to get a ratios from 0 to 100%. And then multiply that by 2 pi to get our angle measurements.
This simply gives us n points on a tiny tiny circle. To get from that to a drawing function that's usable, there's a few transformations that need to occur.
- This circle's radius is 1. You probably want something big enough to show up on the screen. Multiply the output of cosine and sine the the desired radius you want. This would be the distance between the center of your polygon and one of its corners.
- This only generates coordinates that are centered around (0, 0) which is the top left corner. You'll have to add x and y offsets to position it elsewhere.
- As is, this will always start at the 3 o'clock position when drawing points. If you're wondering why my stop sign example adds pi / 16, this is why. Most people think of canonical regular octagons as having two sides that are horizontal and two sides that are vertical. If you start with a point at the 3 o'clock position, there will not be any horizontal or vertical sides.
- Rotating it by half a side length will offset this so that one side will start 1/16th above the x axis and 1/16th below, giving it a vertical appearance.
- While it's not terribly important, note that in mathematics, the positive y axis points up and in most computer graphics frameworks (such as PyGame), it points down. The most evident manifestation of this is that when you offset the angle, it will rotate clockwise, not counter-clockwise.
You can further have fun with this by doing things like multiplying or offsetting the coordinates in multiples of 2 or 3, etc. For example, if you draw a 10-pointed polygon but multiple the radius by .5 for every other point, this will give you a 5-pointed star.
Thought exercise: how would you generate a saw-blade shape?