If you have a cube where the stickers aren't just solid colors, but patterns, then you may have noticed that after solving the cube, the centers don't always orient themselves properly. This minor detail isn't covered in most Rubik's Cube solutions since everyone assumes you have a color cube. How unthoughtful.
Methodology Reasoning
Suppose you have a solved cube sans oriented centers. To rotate the center of one face in a trivial fashion, all you have to do is rotate that face. POOF. The center is rotated. However, now you have the 8 pieces around it in the wrong place. To put those pieces back, you have to undo the move you just made. It seems that you can only have one or the other.
Now, suppose you did your quarter turn to fix the center of the cube. Then, before returning the 8 pieces around it, you switched that center piece with another center, and then undid your first move. Then you returned the original centers to their initial position. You have turned a center, and then unturned a DIFFERENT center. That center and the surrounding edges are now all solved.
What are you talking about?
Ok, practice the following...
- Move the middle row of the cube in a direction.
- Now move a different middle row of the cube in a direction.
- Now undo your first move.
- Now undo your second move.
Now all the centers should be misplaced. Practice this. Practice this until you can predict where the centers will go when you perform this move.
Suppose you have the following set up where the yellow and red center are orientation dependent and must each be rotated 90 degrees.
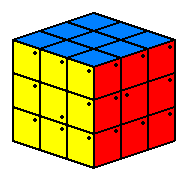
Now shuffle the centers to emulate this:

Now rotate the yellow center (and by "yellow" I mean the center on your cube that corresponds to yellow here) 90 degrees in such a way that it "fixes" it relative to the yellow face.

Yeah, like that.

Now undo the shuffling you did in the first step. Since you rotated the surrounding 8 red pieces, then when the red center returns to the red face, it is correctly oriented...usually.
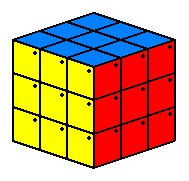
Yay!
Note: This illustrates how to solve the most trivial case where two faces need to be rotated 90 degrees. Typically, several faces will need to be rotated. You can use this move several times in a row. If, for example, you have 3 centers that must be rotated 90 degrees, then you could use this move once to fix one of them, and then use this move a second time to fix the other two. You can also get creative and use other center-swapping algorithms before you do your "fixing" turn.